PID Controller
As discussed in the previous article (controller), the PID is a tool used in industrial control manufacture to achieve the target of the process. The PID controller is one of the controller types used in a control system. It has a special mathematical algorithm called PID. The PID denotes proportional (P), Integral (I), and derivative (D). This controller type is widely used in all automation and control systems. as well as making the process perform in perfect condition.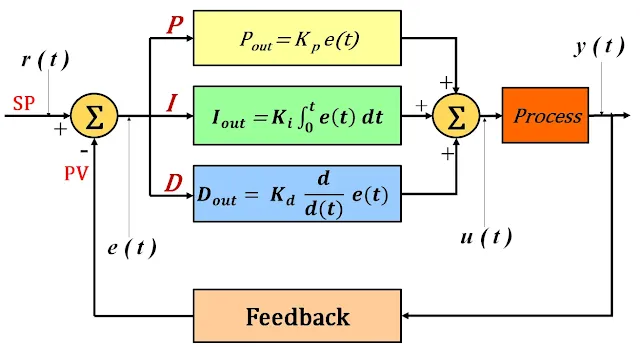 |
| PID Controller configuration |
How does the PID controller work?
Like any controller, the PID controller reads the process values from the
sensors
which are PV signals, and compares them with the preset SP to calculate
the error where the error is the difference between the set point and the
process value (SP – PV). Then it processes that error value to produce an
MV signal which is sent to the process drive to get the desired output. As
the PID controller is a continuous control over time, the error value will
be a function of time. The three factors of the PID controller are
processing the error value in three different ways. The full mathematical
model of the PID controller is as follows:
 |
| PID Controller's equations |
The proportional term.
In the proportional term of PID, the proportional factor deals with the
current value of error which means that it handles the overshoot of the
process output. the overshoot is the maximum value of the process output
over the SP. One of the disadvantages of the on/off controller is that it
has a high overshoot. When the overshoot is high, the system will
oscillate and unstable.
By using the PID proportional factor, and after it is tuned and adjusted,
the overshoot of the process output will be adjusted too. if the
proportional factor is very high, it will make the system oscillate and
become unstable, and if the proportional factor is too low, the system
will be too slow which is not acceptable and need to tune the proportional
part by tuning the proportional factor. The proportional term is the
result of multiplying the error by the proportional gain as shown in the
following equation:
Pout = K p e(t)
Where:
Pout : is the proportional term.
K p : is the proportional gain.
e(t) : is the error as a function of time.
The Integration term.
In The PID, the integration term deals with the old error values over time
accumulated which means dealing with the steady state error value. The
steady-state error value is the difference value between the setpoint SP
and the process value PV (SP – PV) at the steady state where there is no
change in the input or output over time.
The integral portion of the PID control here is pushing the process value
PV to the direction of set point SP and targeting the zero difference
between PV and SP. As the integral part deals with the accumulated
previous values of error, it may increase the possibility of overshooting.
That is why also the integral factor should be tuned. The integral term is
calculated by multiplying the integration of the error which represents
the previous error accumulation by the integration gain as shown in the
following equation:
The derivative term.
In The PID controller, the derivative term handles the expected and the
future value of the error through the rate of change of the error value.
The rate of the error value change is also the slope of the error value
through the process performance. The derivative term of the PID is
calculated by multiplying the derivative of the error by the derivative
gain. As the derivative term predicts the future value of the error, it
may improve the settling time and system stability. The equation to
calculate the derivative term in the PID controller is as follows:
 |
| PID Diff. Part |
In the Automatic
control system, there are very important definitions that should be known. These
definitions are:
- System Response represents the behavior or the response of the system or process over time.
- Rising time (Tr) which Is the time that the process takes from 10% to 90% of the reference value (SP).
- Maximum overshoot (Mp) which is the maximum value of the process response e(t) over the reference (SP).
- Steady State Error (SSR) is the error at the steady state where there is no change for input or output.
What are the advantages of the PID controller?
- Easy and simple.
- It is used automatically without any interference from the operators.
- Widely used in automatic control systems.
- Increase the rise time of the process response.
- Decrease or remove the overshoot.
- Decrease the steady-state error.
What are the disadvantages of the PID controller?
- If the system has noise and because of the proportional term in the PID controller, the value of the noise will be amplified as well as the error value that may cause the system to oscillate and unstable.
- As the PID is a systematic application, it will not suit the non-linear system especially when the dynamic parameters of the non-linear system change rapidly and significantly and push the system towards the instability state.
- Because of the integral term of the PID which affects the steady-state error.
What is the PID tuning?
The tuning of the PID is the adjusting of the PID parameters P, I, and D
to achieve the optimum performance of the process which are increasing the
response, decreasing or eliminating the system overshoot, and minimizing
or eliminating the steady-state error. There are many types of PID
controlling manual and automatic tuning.
What is the Manual tuning of the PID controller?
The manual tuning of the PID controller is a try-and-error technique that
collects data about the performance of the system during the tuning
period. And then then calculates the PID parameters based on the
performance of the process. That method may need fine-tuning to get the
optimum response of the process.
What is the PID automatic tuning?
Many modern PID controller is supported by program software to calculate
the PID parameter based on a routine test. The system will run and
calculate the internal parameter to maximize the efficiency and minimize
the error.


